UQ Physics

Thin lenses

A thin lens is simply two interfaces joined together. A curved interface together with a straight interface forms a plano-convex/plano-concave lens while two curved surfaces form biconvex/biconcave lenses. The distance between the interfaces on axis is assumed to be small in comparison with object, image and focal distances. Vergence theory allows a quick derivation of the propagation of light through any thin lens.

Combining Interfaces

Consider two interfaces, both with refractive indices n, that are cut and joined to form a lens. Light passing through the first interface forms an image at some distance given by the final vergence V_f1 = +n/v. The distance from this image and the second interface is also v (ignoring the thickness of the lens). The light is converging and propagating in the same glass so V_i2 = +n/v. Thus V_i2 = V_f1. Writing the vergence equation for both surfaces:

V_f1 = P₁ + V_i1

V_f2 = P₂ + V_i2

Combining these equations with the relationship between initial and final vergences gives

V_f2 = (P₁ + P₂) + V_i1

The same vergence equation therefore applies for the lens with the power of the system being given by the sum of the individual powers. This is a general result for any combination of interfaces and mirrors provided that the distance between components is small compared to focal lengths and object/image distances.

For thick lenses account must be made of the separation between the interfaces on each side of the lens.

Lens equation

Consider a thin lens in air. As shown above, the power of the lens is simply the sum of the powers of the individual surfaces. The diagram shows a biconvex lens but the derivation is valid for any type of thin lens.

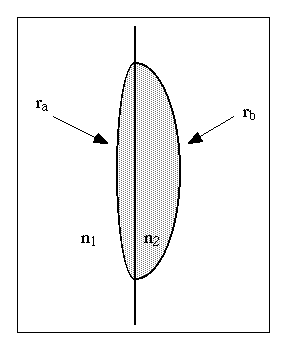
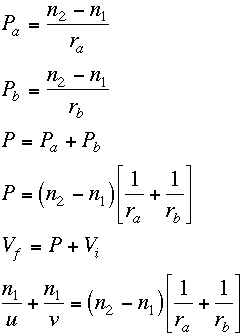
For air, n₁~1,use n = n₂and define f by

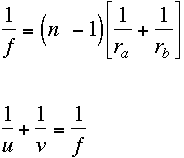
Ray Diagrams for Thin Lenses

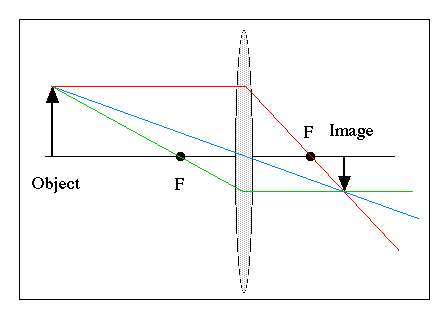
To draw a ray diagram, apply the following rules

Parallel Ray: refracted through focus
Focal Ray: refracted parallel
Central Ray: passes (straight) through

Focal Point

The focal points for a lens are also calculated in the same manner as that for a mirror. The first focal point is the position where light from a point source is collimated (V_f=0). The second focal point is where collimated light entering the system is focused (V_i=0). See if you can determine these locations for a lens.

You should be able to derive the general result that the focal points of any lens in air lie at distances f = 1/P on either side of the lens.

Example - Thin Lenses

Use vergences to determine the power of the following lenses:

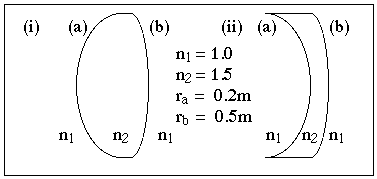
Calculate the position and magnification of an object located 300 mm to the left of each lens.

Example (i)

Step 1. Determine the power of the lens by determining the power of each surface.

P_a = (n_in-n_out)/r = (1.5-1.0)/0.2 = +2.5 D

P_b = (n_in-n_out)/r = (1.5-1.0)/0.5 = +1.0 D

The power of the lens is thus +3.5 D - a converging lens. The focal points can be determined as follows:

First: V_f = 0 => V_i = -P = -3.5 D. The focal point is real (a real point source generates a negative initial vergence) and is located 286 mm to the left of the lens.

Second: V_i = 0 => V_f = +P = +3.5 D. The focal point is real (a positive final vergence focuses to a real image) and is located 286 mm to the right of the lens.

As stated above, these are general results for lenses in air - the focal point f=1/P.

Step 2. A diagram can now be drawn.

Step 3. Determine the initial vergence: V_i = -1/0.3 = -3.33 D

Step 4. Determine the final vergence: V_f = P + V_i = 3.5 - 3.33 = +0.17 D

Step 5. Determine the final position: v = n/V_f = 1/0.17 = 6 m

Step 6. Determine magnification: m=V_i/V_f = -3.33/0.17 = -19.6

The result is that a real image is formed 6 m to the right of the lens (opposite side from the object) that is inverted and 19.6 times larger than the object.

Example (ii)

(Try this yourself.)